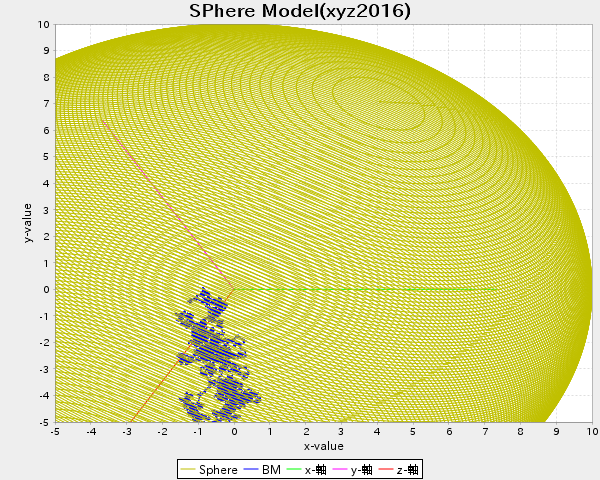
2次曲面上のブラウン運動のドリフト項はその曲面の法線方向に働き、その大きさは平均曲率である。2次元曲面上のブラウン運動の蓋然項(dBtの係数)は、局所座標によらない表現でできる。この2点を理論仕様書(2016版)の参考文献[1](1988年の論文)の結果に従って述べる。この2つの結果はよい結果だとおもうし、一般次元に拡張できる話であるけれど、なぜか(論文のタイトルにComputer Simulationが含まれること、論文の書き方が、なかなか数学としてはよみづらい、ただし結果はあっているという物理屋さんまたは、計算器屋さんの書き方が理由?)あまり、シミュレーションの評価以外はされていないように思う。簡単な微分幾何の知識で、マリアバン解析のある主要な部分(つまり、座標系によらずに、リーマン面上にブラウン運動を構成できること)を結果として与えた(論文の中にはそのような観点での指摘はないが)業績は大きいと思う。ここでは、その証明を上の文献とは独立に与え、またそのサンプルとしてコンピュータシミュレーションで、球面上のブラウン運動を極座標と直交座標それぞれでシミュレーションした結果とその差異のグラフをあたえる。(シミュレーションに関しては、理論上同じになるはずだから単なる計算誤差がこのくらいはあるということを示したにすぎない。)
理論仕様(2016.7)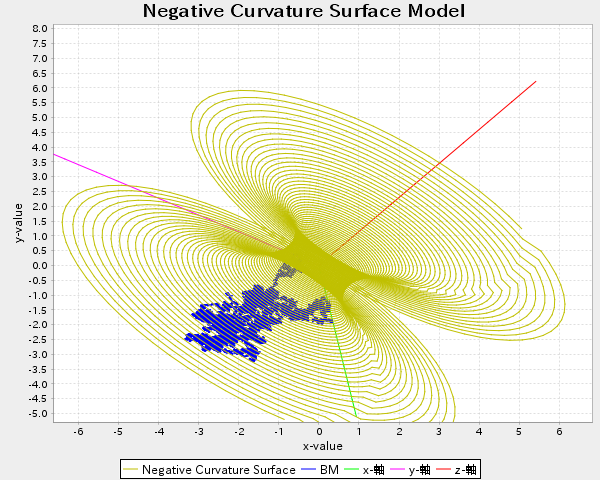 球面、ロバチェフスキー空間、および負曲率を持つ曲面全体(詳しくは、以下の理論仕様をみて)3次元空間内の2次曲面として表現し、その上での測地線および、ブラウン運動の軌跡をシミュレーションできる。3次元空間での、図の拡大、回転、平行移動等の機能をそなえた表示機能を持つ。JAVAで開発しているので、高速である。インストールするのには、若干のJAVAの知識が必要だがEclipseが使える程度でよい。
球面、ロバチェフスキー空間、および負曲率を持つ曲面全体(詳しくは、以下の理論仕様をみて)3次元空間内の2次曲面として表現し、その上での測地線および、ブラウン運動の軌跡をシミュレーションできる。3次元空間での、図の拡大、回転、平行移動等の機能をそなえた表示機能を持つ。JAVAで開発しているので、高速である。インストールするのには、若干のJAVAの知識が必要だがEclipseが使える程度でよい。
 2次曲面上のブラウン運動のドリフト項はその曲面の法線方向に働き、その大きさは平均曲率である。2次元曲面上のブラウン運動の蓋然項(dBtの係数)は、局所座標によらない表現でできる。この2点を理論仕様書(2016版)の参考文献[1](1988年の論文)の結果に従って述べる。この2つの結果はよい結果だとおもうし、一般次元に拡張できる話であるけれど、なぜか(論文のタイトルにComputer Simulationが含まれること、論文の書き方が、なかなか数学としてはよみづらい、ただし結果はあっているという物理屋さんまたは、計算器屋さんの書き方が理由?)あまり、シミュレーションの評価以外はされていないように思う。簡単な微分幾何の知識で、マリアバン解析のある主要な部分(つまり、座標系によらずに、リーマン面上にブラウン運動を構成できること)を結果として与えた(論文の中にはそのような観点での指摘はないが)業績は大きいと思う。ここでは、その証明を上の文献とは独立に与え、またそのサンプルとしてコンピュータシミュレーションで、球面上のブラウン運動を極座標と直交座標それぞれでシミュレーションした結果とその差異のグラフをあたえる。(シミュレーションに関しては、理論上同じになるはずだから単なる計算誤差がこのくらいはあるということを示したにすぎない。)
2次曲面上のブラウン運動のドリフト項はその曲面の法線方向に働き、その大きさは平均曲率である。2次元曲面上のブラウン運動の蓋然項(dBtの係数)は、局所座標によらない表現でできる。この2点を理論仕様書(2016版)の参考文献[1](1988年の論文)の結果に従って述べる。この2つの結果はよい結果だとおもうし、一般次元に拡張できる話であるけれど、なぜか(論文のタイトルにComputer Simulationが含まれること、論文の書き方が、なかなか数学としてはよみづらい、ただし結果はあっているという物理屋さんまたは、計算器屋さんの書き方が理由?)あまり、シミュレーションの評価以外はされていないように思う。簡単な微分幾何の知識で、マリアバン解析のある主要な部分(つまり、座標系によらずに、リーマン面上にブラウン運動を構成できること)を結果として与えた(論文の中にはそのような観点での指摘はないが)業績は大きいと思う。ここでは、その証明を上の文献とは独立に与え、またそのサンプルとしてコンピュータシミュレーションで、球面上のブラウン運動を極座標と直交座標それぞれでシミュレーションした結果とその差異のグラフをあたえる。(シミュレーションに関しては、理論上同じになるはずだから単なる計算誤差がこのくらいはあるということを示したにすぎない。)